Charles Babbage is widely regarded as the father of the computer. However he never actually built his ‘analytical engine’ on which his fame as a computer pioneer now largely rests. So what exactly did he do and what was his legacy ?
Charles Babbage was born on 26 December 1791, the son of a London banker. He was often unwell as a child and was educated mainly at home. He was his own instructor in algebra, of which he was passionately fond, and was well read in the continental mathematics of his day. By the time he went to Cambridge University in 1810 he found himself far in advance of his tutors in mathematics.
After graduation Babbage was hired by the Royal Institution to lecture on calculus. Within two years he had been elected a member of the Royal Society and, with his Cambridge friends, was instrumental in setting up the Astronomical Society in 1820, the first to challenge the dominance of the Royal Society. It was about this time that Babbage first acquired the interest in calculating machinery that became his consuming passion for the remainder of his life. From 1828 to 1839, Babbage was Lucasian Professor of Mathematics at Cambridge.
The 1820s saw Babbage work on his ‘Difference Engine’, a machine which could perform mathematical calculations. A six-wheeled model was initially constructed and demonstrated to a number of audiences. He then developed plans for a bigger, better, machine – Difference Engine 2.
These devices employed the mathematical method of “Successive Differences”. Not only would his proposed device calculate tables (and it included a method of “carrying” from one column to the next) it would also print the results of it’s calculations on paper!
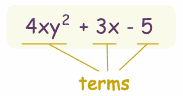
Example of a polynomial. This one has 3 terms
The difference engines were to be used to calculate the value of mathematical expressions called polynomials. These expressiosn ultimately being used in astronomical tables. A polynomial is a mathematical expression made up of terms that are only added, subtracted or multiplied. The engines worked to resolve these equations by analysing the 1st, 2nd , 3rd … nth differences in the series of known answers and then extrapolate for other results. To see afuller explanation of this process refer to the panel below on the ‘Principle of the Difference Engines’
Babbage also worked on another invention, the more complex Analytical Engine, a revolutionary device on which his fame as a computer pioneer now largely rests. It was intended to be able to perform any arithmetical calculation using punched cards that would deliver the instructions, as well as a memory unit to store numbers and many other fundamental components of today’s computers. The remarkable British mathematician Ada Lovelace completed a program for the Analytical Engine but neither it, nor Difference Engine 2, were finished in Babbage’s lifetime. If the Analytical Engine had actually been built, Ada’s program would have been able to compute a mathematical sequence known as Bernoulli numbers. Because of this, Ada is not given credit for the creator of the first computer program however in 1979 a modern programming language, ADA, was named in her honour.
Babbage also worked in the fields of philosophy and code-breaking, as well as campaigning for reform in British science. He died at his home in London on 18 October 1871 aged 79.
Principle of the Difference Engines...
Difference engines are so called because of the mathematical principle on which they are based, namely, the method of finite differences. In general, calculating the value of a polynomial can require any or all of addition, subtraction, multiplication and division.
An advantage of the method of finite differences is that it eliminates the need for multiplication and division, and allows the values of a polynomial to be calculated using simple addition only. Adding two numbers using gearwheels is easier to implement than multiplication or division and so the method simplifies an otherwise complex mechanism.
If the first few values of a polynomial are known, the rest may be calculated using simple repeated addition. The method is illustrated in the diagram above for the function F(x) = x2 + 4. The values of x are shown in the first column incrementing by 1 each time (x = 1, 2, 3, 4 . . .). The values of the function x2 + 4 are shown in the second column with the first four values calculated by mental arithmetic or by hand (5, 8, 13, 20).
The next step is to calculate the first and second differences. The first differences are shown in the third column and are calculated by subtracting successive values from the previous column as shown by the solid arrows flowing from left to right (8-5=3, 13-8=5 etc.). The second differences are calculated by subtracting first difference pairs and these are shown in the last column.
With these initial values calculated the rest of the values of the function can be calculated by reversing the process. The values we wish to calculate are shown below the upper dotted line. For this polynomial, the second difference is a constant (2). To calculate the value of the function for x=5 the constant difference (2) is added to the first difference (7) to obtain the next first difference (9) (red arrow), which can then be added to the last function value (blue arrow) to yield F(5) = 29. This is the desired result, achieved without performing multiplication.
The process can then be repeated to yield the next first difference (11) which may be added to the last function value to get F(6) = 40, etc. Using this method, any second-degree polynomial can be computed this way and, more generally any nth degree polynomial can be computed, using only addition, starting with the nth difference.
Babbage’s Difference Engine No. 2 has ‘registers’ to hold one number from each of the columns in the table (for example 20, 7, 2). It would add the second difference to the first, then add that result to the function value to compute the next entry in the table. There were enough ‘registers’ for seven differences, allowing it to compute 31-digit values for polynomials with terms up to x7.










You must be logged in to post a comment.