You might think the answer to this particular conundrum is one of a combination of simple mechanics plus practice. That is, when learning to ride a bike we train ourselves to cancel out the wobbling we get on starting off by shifting our weight slightly, via the handlebars, and that, once we’re on our way, the gyroscopic effect of the spinning wheels starts to take effect, making the bike even more stable.
However, the dynamics of anything involving spinning bits is never straightforward. It turns out that this is a very tough question indeed.
A TOUGH CONUNDRUM

bikes don’t need riders to stay upright
Even those who have studied the problem in depth do not agree on the finer details of bicycle stability. They do at least agree on one thing: bikes don’t need riders to stay upright; just a push to get them traveling above around 5 miles per hour will do the trick. It’s the source of the inherent stability that causes the arguments. Detailed analysis shows that the much-vaunted gyroscopic effect of the spinning wheels, often thought to explain bike stability (not least by science columnists), is pretty unimportant.

moving bikes stay upright is because of the shape of the forks holding the wheels in place
Surprisingly, the chief reason moving bikes stay upright is because of the shape of the forks holding the wheels in place. These usually point forward towards the ground, so that an imaginary line drawn from them would touch the ground some way ahead of the wheel. It may only amount to an inch or so but this amount of “trail” makes all the difference to bike stability, bringing forces to bear on the wheels that damp out wobbles.
According to various calculations, a bike with vertical forks – and thus no “trail” – would wobble ever faster as it speeds up, becoming increasingly hard to control. Of course, with practice, any bike is rideable – even a unicycle, whose vertical forks give it zero trail. Even so, it’s clear that those outrageously-angled forks on Peter Fonda’s motorbike in Easy Rider aren’t quite so silly after all.
THE GYROSCOPIC EFFECT
Although the stability of a moving bike is NOT related to the gyroscopic effect we thought it worthwhile explaining what it is here …
 A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. Mechanical gyroscopes typically comprise a spinning wheel or disc in which the axle is free to assume any orientation. Although this orientation does not remain fixed, it changes in response to an external torque. The device’s orientation remains nearly fixed, regardless of the mounting platform’s motion.
A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. Mechanical gyroscopes typically comprise a spinning wheel or disc in which the axle is free to assume any orientation. Although this orientation does not remain fixed, it changes in response to an external torque. The device’s orientation remains nearly fixed, regardless of the mounting platform’s motion.
A conventional gyroscope is a mechanism comprising a rotor journaled to spin about one axis, the journals of the rotor being mounted in an inner gimbal or ring; the inner gimbal is journaled for oscillation in an outer gimbal for a total of two gimbals.
The outer gimbal or ring, which is the gyroscope frame, is mounted so as to pivot about an axis in its own plane determined by the support. This outer gimbal possesses one degree of rotational freedom and its axis possesses none. The next inner gimbal is mounted in the gyroscope frame (outer gimbal) so as to pivot about an axis in its own plane that is always perpendicular to the pivotal axis of the gyroscope frame (outer gimbal). This inner gimbal has two degrees of rotational freedom.
The axle of the spinning wheel defines the spin axis. The rotor is journaled to spin about an axis, which is always perpendicular to the axis of the inner gimbal. So the rotor possesses three degrees of rotational freedom and its axis possesses two. The wheel responds to a force applied about the input axis by a reaction force about the output axis.
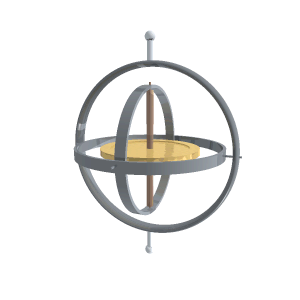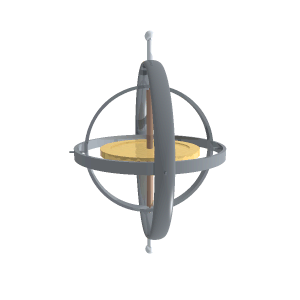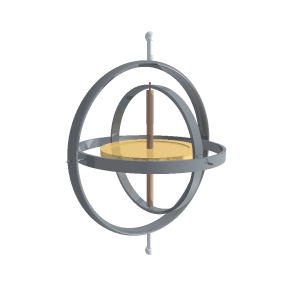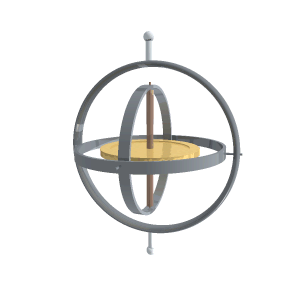
A gyroscope in operation with freedom in all three axes. The rotor will maintain its spin axis direction regardless of the orientation of the outer frame.
The behaviour of a gyroscope can be most easily appreciated by consideration of the front wheel of a bicycle. If the wheel is leaned away from the vertical so that the top of the wheel moves to the left, the forward rim of the wheel also turns to the left. In other words, rotation on one axis of the turning wheel produces rotation of the third axis.






You must be logged in to post a comment.